The Slingshot, a realtime coprocessor for the Rascal

| Brandon Stafford

This post is to preview some of the stuff that I've been working on for the Rascal.

Suppose you want to build a pulse counter so you can tell how fast a motor is spinning. The pulses are coming out of the motor at around 10 kHz, i.e. at 10,000 pulses per second.

The Linux kernel that runs on the Rascal doles processor time out to different programs at 100 Hz, i.e. in 10 millisecond chunks. For example, the Rascal is constantly running a webserver, but also a program that watches for new USB hardware. The Linux kernel schedules those different programs so that they can share time on the same processor. If you were to add code that checked whether a pulse had arrived, it would share time with the rest of the processes running. With this kind of process scheduling running, reading pulses 10 times per second can be done, but reading pulses at 10 kHz is hopeless.

How do we think about this kind of stuff?

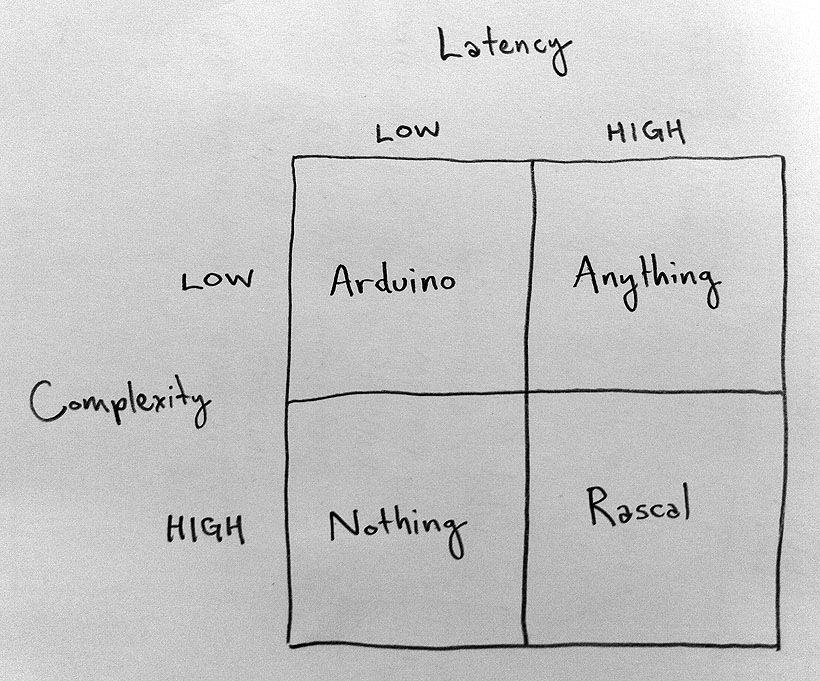
In my mind, I divide tasks into four groups:

  1. Simple and high latency is OK, like tripping a relay to drop a box over a turtle. Any microprocessor can do this.
  2. Complex, but high latency is OK, like image analysis or serving web pages. The Rascal wins at this.
  3. Simple, but low latency is required, like counting pulses from a motor. A microcontroller like the Arduino wins at this.
  4. Complex, but low latency is required, like using facial recognition to pilot a drone toward a target in a crowd. We can't do this on one processor.
##### Diagram that shows what kind of device to use for different tasks #####

In theory, you could change the Rascal's operating system so that the scheduling interval was much smaller, so you could actually check for pulses much faster. The problem with this approach is that every time you stop a process to run your pulse counting program, you burn some time in the switch. Eventually, your system is spending more time switching processes, and your pulse counter starts missing pulses.

Codename Slingshot

A better approach is to use a secondary processor that can handle the low-latency stuff. I've been prototyping this kind of realtime coprocessor as a shield that can plug into the Rascal's headers. For lots of tasks, you could use almost any microprocessor, so long as it doesn't have an operating system. To make things easy, I'm prototyping with an Arduino kit. In the long run, I will probably use a small ARM processor, maybe something like the Cortex M3 used on the Arduino Due. For the meantime, I'm using an Arduino Uno and calling the project codename Slingshot. (Thanks to Dan Beyer for the naming suggestion. He thought a slingshot was the sort of accessory a rascal would keep close at hand.)

In the pulse counter example, the Slingshot counts the pulses very quickly. When the Rascal has a 10 ms slice available, it asks the Slingshot for the count. The Slingshot dumps the answer into its I2C hardware, which talks to the Rascal while the Slingshot keeps counting. In the long run, I would like the Rascal to come with a Slingshot built in, and with a pile of different programs available on the Rascal. If you want a pulse counter, you just select the pulse counter option, and the Rascal drops it onto the coprocessor for you.

The picture below shows the first attempt at the Slingshot. It's just an Arduino with some parts missing, but I think the functionality will be great.

##### The Slingshot running off the Rascal's power supply, connected to the Rascal via I2C #####

I've left out the original headers and the power circuitry from the Arduino kit. For the power connections and I2C, I soldered pins in the open holes. These pins allow the Arduino to draw power from the Rascal's power supply and talk to the Rascal using I2C.

Anyway, this marks the beginning of the Slingshot. I think the Rascal/Slingshot combination will be powerful when the Slingshot is done.

Other folks doing this kind of thing

I would remiss if I didn't mention that lots of other people have done this sort of thing before. In the open source hardware world, there's the Wyolum Alamode board, which is an Arduino that plugs into the Raspberry Pi and can talk over the serial port. One of the guys behind the Alamode, Kevin Osborn, works out of our local hackerspace here in Somerville, so I've talked this stuff over with him a few times.